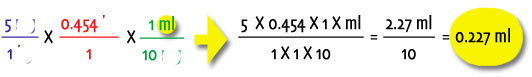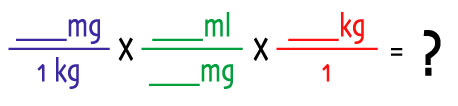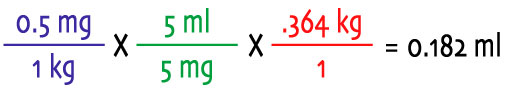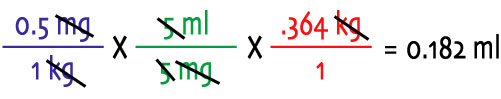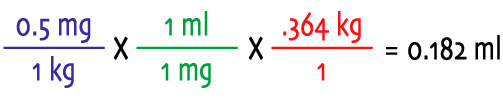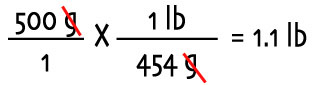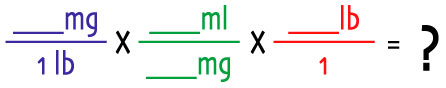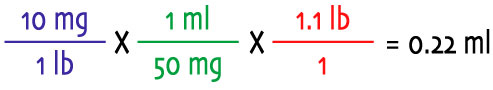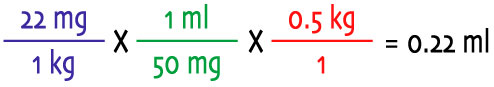Medicine Calculations for the Mathematically Challenged

If you're here because you're trying to save a few bucks, just see your vet. It really does end up being cheaper if you get it right the first time (Please consider reading this to understand why). But maybe you're obstinate or want to confirm your vet's dose (which, I've recently found, due to an experience a friend of mine had involving 10X the recommended dose of chloramphenicol, isn't such a bad idea: Vets are People Too).

We'll first start with a math lesson:

When calculating any dosage, you will need the following:

The actual recommended dosage. This usually appears in the form of, for example, "5 mg/kg."
Your rat's weight. Ideally this will be in grams (not ounces, not pounds). If you must do pounds or ounces, 1 lb is 454 grams and 1 oz. is 28 grams. Multiply your rat's weight in pounds by 454 to have his weight in grams. Multiply your rat's weight in ounces by 28 to have his weight in grams. And then once you have his weight in grams, divide by 1000 to obtain your rat's weight in kilograms because your units will need to match up. Dosages are generally given in "mg/kg" so you want your rat's weight to be in kg.
The suspension information. This usually looks like "10 mg/ml" though if you are dealing with a solid substance, you may just have "10 mg." In order to have a suspension of a solid, you will need to add some liquid that can be safely mixed with the solid you're trying to use (and you will want to crush the solid to turn it into a water-soluble powder) and you will want to measure the liquid you are adding, in mls, and include it in your calculations.
A clear head. Yes, it's math, but chances are you've at least taken basic algebra and I can assume you know where the multiplication and division signs are on your calculator. I am first going to show you why setting it up the way I set it up works. Then I'm going to have a nice set-up where you just write in your information and do the math. If you understand why it works, you won't have to keep coming here. Plus, it's always nice to know why you do things the way you do.

Now that you have all the information you need to calculate your rat's dosage, you need to assemble it in a way that will result in a number that "makes sense." What I do, to keep myself straight, is to start with the actual recommended dosage. I do this because I have to start somewhere and it seems like a good place to start :o)

Using the numbers from above (so as to avoid confusion):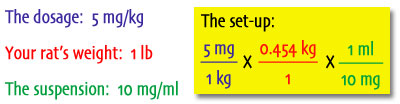

Note that the set-up is set up in the way it is set up (which is a lot of setting up for one sentence) for a reason. What I am doing is cross-matching the information based on the initial numbers "5 mg/kg."

I want my "kg" numbers to be diagonal from one another:

This way numbers with like units cancel out. (For your convenience I blurred out the parts we're not looking at for this example).

I also want my "mg" numbers to be diagonal from one another:

Again, numbers with like units cancel out. (For your convenience I blurred out the parts we're not looking at for this example).

And you can do that for the same reason why you can assume that X ÷ X equals 1. 2 ÷ 2 = 1 and 2002 ÷ 2002 equals 1. And every number (whether a number or whether it's denoted by X) divided by the same number will always equal 1. Think of the units "mg" and "kg" as X and it should make sense.

But there aren't two instances of "ml" are there? There doesn't have to be. When you're calculating the amount of medicine you are to give your rat, you want to know how much, in mls (or ccs) to give your rat. When you get done multiplying and dividing all the numbers, that's what you end up getting: A number that "makes sense" that tells you how many mls (or ccs) your rat needs:

Now look back up at the two examples where you were cancelling the kgs and the mgs out: When you looked at just the kilograms you ended up with 0.454 and no units. When you looked at just the milligrams, you ended up with ½ and no units. 0.454 divided by 2 is 0.227 (no units). Multiply that by your 1 ml and now you have 0.227 ml. And that's the same number you'd get if you were to take all the numbers in the "set-up" (above), multiple all the numbers across the top row and divide by all the numbers across the bottom row.

How'bout some examples:

Example #1

Step 1: Don't panic!

Step 2: The recommended dosage is 0.5 mg/kg so you know the rat's weight can't be in ounces. The first thing you do is multiply 13 ounces by 28 grams per ounce to find that your rat weighs approximately 364 grams.

Step 3: But wait! The recommended dosage is 0.5 mg/kg and you just found your rat's weight in grams so you divide 364 by 1000 to get 0.364 kg.

Step 4: So far, so good but you have a 5 mg pill. It's a pretty small thing all things considered so even if you just stop here and do the calculations (0.5 mg/kg X 0.364 kg - the kg cancel out and you are left with 0.182 mg) you realize that there is no reasonable way to cut out 0.182nd of a pill. So you say, "OK, I should add some liquid" and thinking that 5 ÷ 5 calculates to a nice easy number, you add 5 ml of water to your calculations (and you crush the pill into a fine powder and mix it with 5 ml of liquid).

Step 5: Now you're ready to go. Set it up:

Step 6: ...and do the math:

And yes, I mixed up the mg/ml and kg parts. That's because the order doesn't really matter. As you can see, I still have it so that like units are diagonal from one another:

Or I could do it like this. After all, I chose "5 ml" because I knew 5 ÷ 5 = 1 so I can just use "1s" in place of the "5s:"

Example #2

the RMCA

Step 1: Don't panic!

Step 2: I tricked you! Most dosages, when you look them up in the literature, are given in mg/kg but there are some sources that, geared toward an American metric-system hating audience, will list the dosage in mg/lb. What to do? Well, you can convert the dosage into mg/kg:

...or you can convert your rat's weight to lbs:

Step 3: Now you have a dosage in mg/lb, and you've figured out how many lbs a 500 gram rat is. You also already have a suspension so you needn't worry about creating one. That means every unit has a diagonal counterpart (except for the thing you're trying to find: the mls) so you're ready to go. Set it up:

Step 6: ...and do the math:

Or if you figured out how many mg/kg 10 mg/lb was, you could do it this way:

Great! You should now be an expert! Or, if like me, you'll just head to your little piece of paper with this on it for a subtle reminder so you can adhere to "Step 1: Don't Panic!"

Now for some dosage charts for your convenience:

Calculations for Vetafarm Psittavet Injectable Doxycycline

Calculations for Medpet's DoxySyrup

Calculations for Baytril 10%

tip: When navigating through the RatTails,
clicking on the image that looks like the image above
will take you back to this table of contents!

Disclaimer: There are many non-sarcastic accounts and tips on the web regarding rat care. This is not one of them. These are merely accounts of our experiences with rats, our perceptions of these experiences, where we've failed and where we've succeeded. These accounts are here for two purposes:

1) To entertain.

2) To help avoid repetition of mistakes

Remember! Your rat is not a science project, he is your friend!

All content contained herein © 1996-2007 by Andrew Waltz, Nathalie Baldwin, & the rats of RatRaisins, Inc.
Use of images and/or text without permission is prohibited.